Cauchy stress tensor

This is a topic that is halfway between Physics and Engineering. We are going to deal, in a very simplistic approach, with how the 3D bodies get deformed, but we will alternate between 3D and 2D for visualization issues. Suppose we have a body that occupies a region of space $\Omega$ and suffers an small transformation into a new region $\Omega'$ in a very general way, that includes deformation, traslation and rotation. We interpret that every particle of the body which in the initial state was in position $x\in \Omega$ gets transformed to $T(x)\in \Omega'$

If we think of the transformation as being the resulting action of forces applied on the constituent particles of the body, and we assume that these particles were initially at rest (a solid) we can state that the forces in every point $x$ are approximately:

for some constant $\lambda \in \mathbb{R}$

This is because we can look at $T$ as the result of a continuous transformation $T_t$ depending on a parameter $t$ such that $T_0=I$ and $T_1=T$. This way, $\alpha(t)=T_t(x)$ is the curve describing the evolution of particle $x$, and by Taylor expansion we have

and since particles were initially at rest

where we are assuming, also, that the body has constant density $\mu$.

Studying the whole transformations is complicated, non linear. So we better take care of the local study of every point, assuming that the transformation is very small, as we usually do (it is the same simplification that we do when we pass from studying the curve described by a particle to the tangent vector of that curve). We can imagine that every point $x$ is surrounded by a sphere of very near points $y$, and we want to know how the latter get transformed. That is, we center our attention over $x$ and $T(x)$, and watch the relative displacement of the surrounding $y$s. In the end, this is like saying that a vector $v$ leaving from $x$ is associated with

since, as we observe in the picture on the right, $v$ is associated with

So, what is the physical meaning of $dF_x$? In the same way that $dT_x$ (usually called deformation gradient) describes us the infinitesimal transformation of an infinitesimal piece of the object, $dF_x(=dT_x-I_x)$ tells us, in some sense, the contribution to deformation applied to the piece in every direction. This is the precursor of the Cauchy stress tensor. We can think of it like a linear map that tells us how directions get transformed into new directions. That is, the vector that we have to add to every direction to obtain the new one. We will call it deformation force.

But now, since we concern only with deformations, it would be good if we can remove the rotation part (the traslation part is removed by derivation), but this is allowed by the polar decomposition. We have that

where $R$ is a rotation matrix and $U$ is a symmetric matrix called the right stretch tensor, and it contains the relevant information about the pure deformation. Observe that if we had begin with a transformation such that $R_x=I$ for our point of interest $x$, or if we multiply our original transformation by the constant matrix $R_x^{-1}$, then the matrices $dT_x$ and $dF_x$ would be symmetric, and therefore, diagonalizable.

So let's assume $dF_x$ is symmetric and go back to the physical meaning. If we change to the diagonal basis, the matrix $dF_x$ is telling us that in every main direction going out the particle $x$ we are experiencing a "deformation force" (I think that the technical name is stress) parallel to that direction. Something like pressure when we are under water, but not necessarily the same for every direction, and not necessarily inward. The result is a non-symmetric scale change.

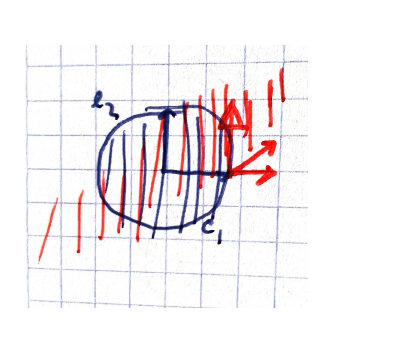
But what if we continue in our original basis? When we focus on a direction going out the center point, we assign a vector whose meaning is, again, the deformation force'' or stress'' that suffers the infinitesimal piece of the body around $x$. This vector can be decomposed in two: a vector $v$ parallel to the studied direction, and other $v_{\perp}$ perpendicular to it, that tells us how we must displace the plane orthogonal to the studied direction. It looks as if you need four numbers to describe the deformation, but in the other basis you only needed two!

Here is needed that you make a mental effort to see that you have the same deformation information that giving a special basis and two scalars meaning the scale change in every direction. Because the special basis itself has to be specified (in the plane case, angle), so you actually need three numbers. And on the other hand, the lateral displacement of the orthogonal planes to every main direction must be equal, as you can understand, intuitively, in the picture below (becauser there is no rotation!):

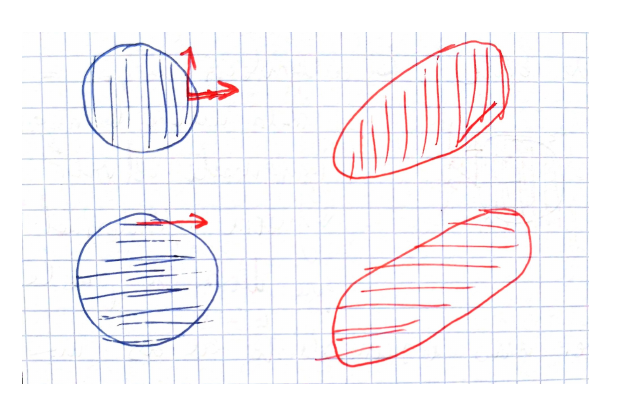
so you actually need tree numbers, again. This is the explanation that Cauchy tensor being symmetric.

Finally, only say that this is a very simple approach. Force and deformation are not so simply related, because it depends on the material we are using. But the important idea to get clear is that deformation is a new kind of information, not so simple like scalars and vectors. We need a tensor.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es